
| グループ別最大増分値の検討 各グループ毎の最大増分値(5分間あたりの最大ウォッチ数)はそのグループのヲタの特性もあり比較することは難しい。グループによってはいわゆる箱推しと呼ばれるグループのどのメンバーでも応援するというファン層が多いところもあれば、個々の個人を応援するファンが基本となっているグループもある。しかしながら基本的にはそのグループを応援するファンによってウォッチ活動は支えられていたわけだから、複数のメンバーがウォッチバトルに参加していたのであれば、その各メンバーの同日、同時間に発生したウォッチ数合計の最大値がそのグループの持っているポテンシャルと考えられる。 |
|
| 検討方法 検討方法としてはそれぞれのグループの最大値が発生したと時間帯を最終日の21:00〜24:00と予測する。しかしながら、この時間に発生する最大値は最終日の終了間際に発生するという極短時間に起きるケースが想定される。それに比較すると上西は終了前1時間程度同じぐらいの値で推移しており、その時間帯に最大値が発生している。したがって上西のデータとして比較対象となる最大値は、少なくとも1時間程度は継続できるものでなければならない。これらの点から考えると、最大データとして考えることができるものは、最終日の終了間際にのみ発生するような特異なデータを除いた、正規分布していると考えられるデータ母集団の中から、継続的な発生の可能性が想定できる値の中での最大値を選択する必要がある。 そこでデータの検討範囲はそれぞれのグループの対象日の19:35〜24:00と21:00〜24:00の2つの範囲で検討し、それぞれの平均(μ1,μ2)と標準偏差(σ1、σ2)を求める。ここで仮に予想最大値(M)をμ2+σ2×2として計算しておく。そしてそれぞれの区間の正規性を検討し、正規性が認められない場合には、極端に高い値や極端に低い値など正規性から逸脱するようなデータを除いて、どの範囲のデータで算定すれば正規性が認められる範囲となるか検討する。最低限のデータを除外して正規性が認められる範囲を算定した後に、各対象時間帯の平均(μ3,μ4)と標準偏差(σ3、σ4)を再度求め、μ3+σ3×2、μ4+σ4×2を計算し、高い値になる方のグループを最大値が発生する母集団と見なし、その母集団での累積分布関数から1%有意水準(危険率1%)で発生可能となる値を最大値とする。もし最初に計算した予想最大値:Mを1%有意水準で検定してその母集団での発生が否定されない場合はMを最大値とするが、そうでない場合は累積分布関数で発生確率が99%となる累積分布関数の逆関数で求められる要素:xとなる値を最大値と考える。なお、データ要素の正規性の検定にはシビルワークス社提供のフリーソフトである正規性検定ツールを利用し、有意水準1%のD'Agostino and Pearson検定(K2検定)で検定した。 統計的な用語について馴染みにない方向けに、以下に上記の検定方法を採用した理由及び、用語の概略について説明しておく。 |
 |
|
||||||||||||||||||||||||||||||||||||||||||
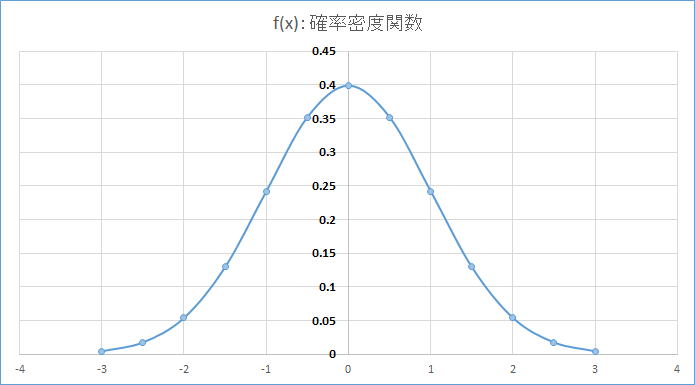
| 正規分布について 上のグラフはExcel2013のNORM.DIST関数を用いて平均(μ):0、標準偏差(σ):1の標準正規分布となる確率密度関数を求めグラフ化したものである。基本的に正規分布のグラフは平均を中心とし、上のような左右対称のグラフになる。一般的なデータの測定結果をグラフ化した場合、必ずしもこのようなきれいに左右対称の正規分布の形にデータが分布するとは限らない。その為、測定されたデータが正規分布として考えられるデータかどうかを何らかの方法で検定する必要がある。今回は上で述べたようにフリーソフトであるシビルワークス社の正規性検定ツールを用い、計測された増分値データに正規性があるかどうかを確認することとした。 |
|||||||||||||||||||||||||||||||||||||||||||
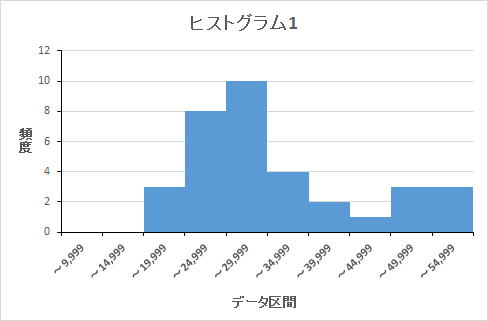 |
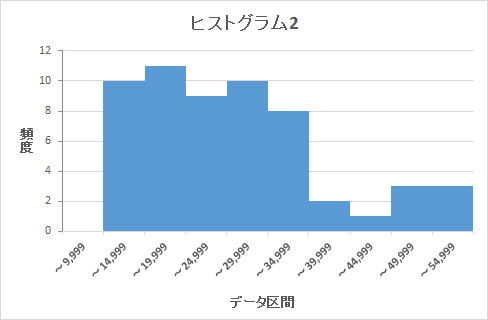
ヒストグラムの作成 一般的に測定されたデータが正規分布をしているかどうかを判断するには、ヒストグラムを作って検討することが多い。ヒストグラムはデータを区間分けして、その区間毎にどれだけのデータが発生しているかを検討するための方法である。一般的に正規分布が予想されるデータでは、左記のヒストグラム1のように中心部分の頻度が高く、左右に離れるにつれて頻度が低くなるケースが考えられる。 しかし、必ずしもそのような形になるデータばかりではない。ヒストグラム2のようなデータ分布となった場合、正規分布ではないと言い切れるかどうかは判断が難しい。その為に正規分布かどうかを判断するツールとして、上記に記載した正規性検定ツールを利用した。上記検定ツールは実際に測定したデータを用いてその正規性の判定ができるものである。 実際に左記のヒストグラム2の元データを有意水準5%のK2検定で判断すると「正規分布ではない」との判断になったが、データ区間:50,000〜54,999に含まれる2つのデータのうち、最大値となる一つ除くと「正規分布の可能性がある」との判断になった。 一般的にウォッチバトルの最終日のデータでは、最終日の終了間際にその時間帯だけ参加する人や、最後の5分間だけ頑張ってウォッチ数を上げるといった行動を取る人が多かった。そのため、継続的にウォッチし続けられる最大値を統計的に求めるには、そういう特異なデータを除外した上で、発生しうる最大値を検討する必要がある。 したがって、統計的に計算して求める最大値としては、正規性検定ツールでそういった特異なデータを除外した上、正規分布の母集団として認められる範囲のデータを特定して、それを用いて検討した結果、発生しうる最大値を算定することとした。 ちなみに、左記のデータは5月3日のHKT:穴井のデータを元にして作成したものであり、ヒストグラム1が21:00〜23:50、ヒストグラム2が19:10〜23:50の増分値をヒストグラムにしたものである。 いくつかのメンバーのデータを検定したが、最終日でない日の21:00〜24:00の間のデータは、どのメンバーのデータも有意水準5%のK2検定で「正規分布の可能性がある」との判断になることが多かった。 |
||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||
グラフ1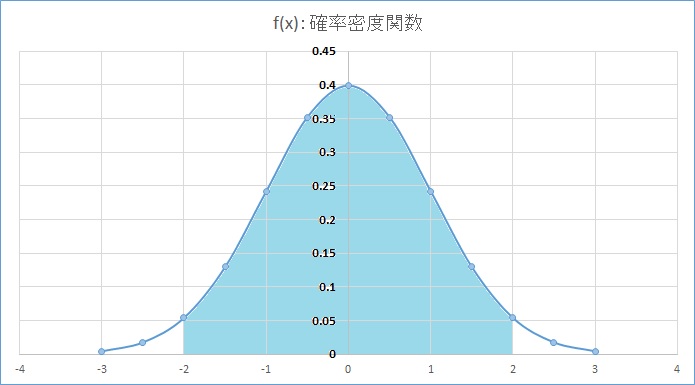 |
累積分布関数 一般的に正規分布している母集団のデータでは平均(μ)、標準偏差(σ)に対して、μ±σの範囲に68.27%、μ±2σの範囲(グラフ1の水色の部分)に95.45%、μ±3σの範囲に99.73%の値が含まれることが知られている。また、一般に両側検定で利用される95%の値が含まれる(5%有意水準)となる範囲はμ±1.96σ、99%の値が含まれる(1%有意水準)の範囲はμ±2.58σということが知られている。 累積分布関数は正規分布となる確率密度関数を積分したものであり、言い換えればその要素(増分値):xを最大値としてその値までに含まれる要素が、全体のどれだけの割合になるかを表わしている(グラフ2の水色の部分)。その為、上の表ではμ(0)までの累積分布関数は0.5、μ+2σ(0+1×2=2)の累積分布関数は0.977249868となっているが、μを最大値と考えると全体の50%、μ+2σを最大値として考えるとその値までに全体の97.72%の値が含まれるということを意味する。今回は発生しうる最大値を求めることを目的としているので、片側検定で1%有意水準で検定する場合、累積分布関数として99%の値が含まれる値を求めることよって検定することができる。つまり、累積分布関数の逆関数を利用して平均、標準偏差から累積分布関数が99%となる要素(増分値):xの値を求める。 そうやって要素(増分値):xの値を計算によって求めることができれば、その値が1%有意水準(危険率:1%)でその母集団において発生しうる最大値だと判断することができる。但し、この計算から求める値はあくまでも母集団が正規分布しているデータである場合に妥当性を持つものであり、元のデータを正規性検定ツールで検定し、特異なデータを除いた後に各データを用い平均と標準偏差を求める必要がある。 仮にそれより大きな値が発生していたとしても、それはその母集団から自然発生的に起きた事象とは言えず、意図的もしくは人為的に何らかの方法で発生させた事象というしかない。もしくは母集団を別にして発生した現象だと言えるかもしれない。 今回、累積分布関数の逆関数としてはExcel2013でのNORM.INV関数を用いて値を求めることとした。 |
グラフ2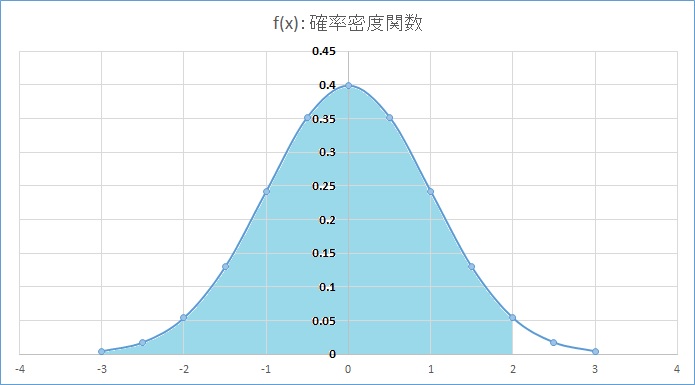 |
|
| 以上の方法で算定した正規分布データとして考えられる母集団から求めた最大値、平均、標準偏差を基準にして、HKT、NMB、SKE各グループにおける最大増分値を推測し、それをグループ全体が持つのポテンシャルとした。その各グループの結果を用い、5月3日における上西の予想データの妥当性、及び実測データの異常性を検討する。 |
|
| HKT:グループ最大増分値予測 | NMB:グループ最大増分値予測 |
| SKE:グループ最大増分値予測 | 穴井最終日データの検定 |
| 上西最終日データの検定 | |
 トップへ戻る トップへ戻る |