
| 仮想データ1 ここでは高柳のデータを中心に様々な化粧を施し、それと上西のデータを比較することで検討を進めたい。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
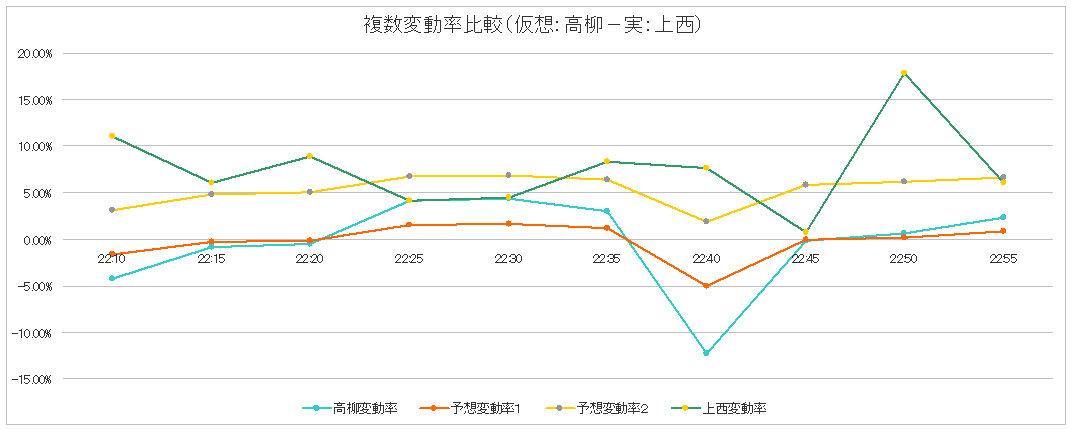
ここで検討したのは高柳のデータに人工的に何らかのデータを加えた場合、どのような変動になって変動率に影響を及ぼすのかを検討した。まず第一に5分毎のデータに毎回一定量を加えた場合を人工値1として作成した。人工値1は毎回250,000の固定値を与えるものとした。表では測定値との合計を合計値1として表示している。 しかし、その変動は表中の人工変動1として表示しているが、高柳の測定値の変動と何ら変わりない。これは当然のことで変動はあくまで直近5分前からの増分との差をとっているだけなので、両者に同じ数を加えたところで差分に変化が発生するはずもない。グラフは変動率によるデータ推移であるので分母となる値が増えることにより振幅自体は小さくなる。高柳のグラフ(水色)と予想変動率1(オレンジ)のグラフとの比較でその違いを読み取ることができる。 そこで次に考えたのは加速度を持ったデータを加えた場合である。それを人工値2として加えてみた。人工値2は初期値250,000で、それに毎回前値を1.08倍する加速度を与え増加させた数字である。これを5分毎の測定値に加えた値が合計値2である。そしてこの合計値2の変動をとったのが人工変動2に当たるが、これはすべてプラスの値となった。これらの値及び上西の測定値を元にして、変動率を計算しグラフ化したものが上のグラフである。 上のグラフ中緑色で示したのが上西の変動率の推移であり、黄色で示したのが人工変動2を元にした変動率の推移である。先ほど示した高柳(水色)の変動率が-12.26%〜4.32%で推移しているのに対し、上西の変動率が0.77%〜17.86%の間で推移しており、ほとんど重なるエリアがない。 しかし、仮想データとなった人工変動2を元にしたデータでは変動率が1.88%〜6.82%となっており、すべての値が上西の変動率の範囲に含まれる。つまり言い換えれば上西のデータと合計値2のデータは同じような変動で増分値が推移していると言える。 次は逆に上西のデータを加工し、より実態に近い値を推察してみる。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 前へ |  トップへ戻る トップへ戻る |
次へ |